浮點數與科學記數法
之前講過的定點整數,只是對整數的一種存儲,諸如3.14這種只能存成314,之後那就要想辦法存下“小數點在最高位3和次高位1之間”這個信息 放心吧,計算機怎麼也不會真正的保存小數點,科學記數法就發揮了很大的作用。
十進制下科學記數法,就是將一個數表示成
number=a?10n 這種形式,並且對a做限定 1<=|a|<10 比如 3.14=3.14?100314=3.14?102 如此一來,相當於默認了小數點位於a的最高位和次高位之間,那麼只要存下了a*10^n也就不需要存小數點了 問題?為什麼要乘10? 比如一個數字3.14,3.14?10=31.431.4?10=314314?10?1=31.4
看看看,小數點在運動哦~就醬
二進制下有點不同
number=b?2n0<=|b|<1 比如(除了2之外都是用二進制表示)10.01=0.1001?22 還可以乘別的數來表示,比如10.01=0.1001?41 只不過4的指數每變化1小數點就要移動2格 這種對b的規范,默認了小數點的位置 進一步,如果默認了乘的數就是2的話,那麼需要存儲的只有小數b和指數n了,我們叫這個乘數2為基值
浮點數的格式
對於一個有小數部分的二進制數number,我們寫出規范化的科學記數法的形式number=b?2n 0<=|b|<1 那麼number就可以用b和n兩個數來存儲,同時默認了兩個條件
n是需要乘的2的指數 b在0到1之間,也就是說b只能是0.XXX的形式 對於n來說,n就是一個整數 b是0.XXX的形式,那麼我們就只需要存儲“0.XXX”的“XXX”部分就可以了,這也是一個整數的形式 起個規范化的名字,我們稱 n 為階碼,稱 b 為尾數 看圖
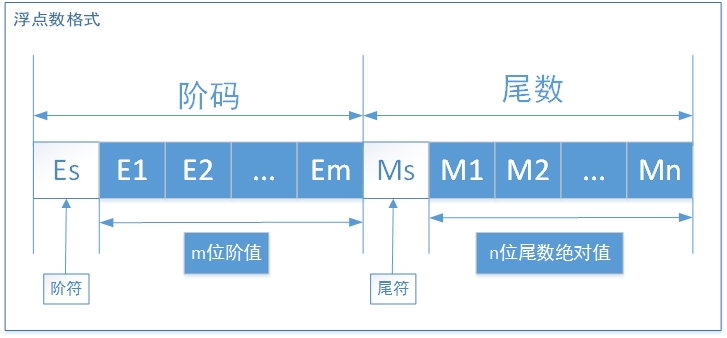
考慮到正負的問題,分別留出一位Es和Ms作為符號位,同樣是0代表正數,1代表負數
規范化格式
問題又來了?依舊用10.01來舉例10.01=0.1001?2210.01=0.01001?23 也就是說,盡管尾數已經在0到1之間了,我依舊可以移動小數點,再順勢改變一下階碼的值,同一個數存起來就有多種存法 於是對於計算機內存儲的時候,還需要進一步規格化 很簡單,你想移動小數點,規格化了之後就讓你無法移動小數點 即規定:M1必須為1 那麼10.01就只能存成0.1001?22 的形式了
浮點數表示的問題
但是,這種規格化也帶來了另一個問題,那就是在實現規格化的過程中,我們總是想讓M1為1,就需要移動小數點,也就需要改變階碼的值 問題是,你移動了多少多少位來使得M1為1,但是要改變的階碼的值卻超出了階碼的表示范圍!!就是說階碼的表示范圍是有限的!! 這個問題就是浮點數不得不直接面對的問題了,另外尾數的位數限制也是浮點數表示法所固有的精度問題 舉例,取E1-E3共3位來記錄階值,Es一位記錄階符,M1-M3共3位來記錄尾數的絕對值,Ms一位來記錄尾符
最大值:M1-M3均為1,Ms為0表示正,E1-E3均為1,Es為0表示正,即MaxValue=0.111?27=1110000 最小值,即最大值的Ms取1表示負,即MinValue=?0.111?27=?1110000 規范化表示下最接近零的正數M1取1,M2取0,M3取0,Ms取0,Es取1,E1E2E3均為1,即ClosestToZero=0.100?2?7=0.00000001 規范化表示下最接近零的負數自然就是ClosestToZero=?0.100?2?7=?0.00000001 問題就是:
超過了最大值最小值,無法表示,稱為上溢。這個可以理解,畢竟就算整數也有上限下限。一般運算超過了上限下限會出錯,而不像整型那樣截斷。 比較獨特的地方在於,比“最接近零的數”更接近零的數無法表示。原因在於階碼范圍的限制。在這個靠近零的狹小范圍內,用浮點數來表示都是0,也就是機器中為全0來記錄,盡管真實的數值可能很接近零但不是零,然而計算機表示的能力有限,太小的數無法表示,成為“機器零”,稱為下溢。 最後就是精度的限制與損失。精度限制的原因是尾數的位數有限,而精度的損失一方面來源於“規格化”時小數點的移動,這使得某些數位可能移到了尾數表示范圍之外,如 101.01=0.10101?23=0.101?23 後兩位01沒有了,因為尾數總夠3位只能保存前面的3位;另一方面來源於十進制轉換成二進制所固有的限制,比如 (0.25)10=(0.01)2 這樣是沒有損失的,但 (0.2)10=(0.0011001...)2 你會發現十進制的 0.2 根本無法用二進制來完美的表示。其實固然如此,就好比十進制無法完美表示三進制的0.1一樣。(0.1)3=1/3=(0.3333333...)10
IEEE標准
通常
float為 4 Byte = 32 bit , 即float中Es,Ms各占一位外,E1-Em和M1-Mn共占 32 - 2 = 30 位。 double為 8 Byte = 64 bit ,即double中Es,Ms各占一位外,E1-Em和M1-Mn共占 64 - 2 = 62位。 那麼如何分配 n 和 m 的值,這就需要一個統一的標准
美國電氣與電子工程師協會IEEE(Institute of Electrical and Electronic Engineers)為了便於軟件的移植,為采用軟件對浮點數運算時發生特殊情況進行處理提供支持,並鼓勵開發出面向數值計算的優秀程序,於1985年推出了“浮點數表示及運算標准”,即IEEE標准754。
其設計者Kahan因此榮獲了1989年的圖靈獎。
IEEE標准如下
最高位為尾數符號位S 次高位段為 用移碼表示的 階碼E 低位字段為 尾數F 基值為2 基本單精度格式:E占8位,F占23位,共32位 基本雙精度格式:E占11位,F占52位,共64位 擴充單精度格式:E>=11位,F>=31位 擴充雙精度格式:E>=15位,F>=63位
還有一些很奇怪的地方,我盡可能按我的理解解釋一下
階碼采用移碼表示,為的是便於比較。因為當浮點數進行加減的時候,必須在統一了階碼的前提下才可以對尾數進行加減。 單精度格式階碼E為例,其范圍是1~254,也就是單精度階碼 E : 00000001 ~ 11111110 偏移值是127,也就是說實際的階碼值是 1-127 ~ 254-127 即 -126~+127之間,也就是單精度階碼 E : 10000010 ~ 01111111 此時的表示方式就變成了補碼 上一條中偏移值是127可能需要再解釋一下。普通的移碼的定義是,為了使得最高位為符號位下編碼的二進制正負直接可以直接比較,我們把最高位取反來得到移碼,而最高位取反的操作,以4 bit的“0000”為例,也就相當於加上了“1000” 即 2^3=8,對應上條來說,偏移值本應該是128。但別忘了,移碼的最終目的是為了使二進制編碼的數字可以在正負之間直接比較,達成這個目的同樣可以用加上2^3-1 = 7即“0111”來達到,對應可解釋上條中的偏移值為什麼是127也同樣可以了。 階碼E中上有 全0 和 全1 沒有編入,這個有特殊的用途,見下面的表格 還記得規格化的要求嗎,即M1=1,既然強制了M1=1,那麼就不需要存儲了嘛,所以IEEE標准754引入了“隱藏位”技術,即不存儲規格化要求了的M1=1,這樣就使得尾數多出一位來,精度也就提升了一位。
IEEE的五種實體
還記得沒編入階碼的 全0 和 全1 嗎,這兩種狀態分別與尾數的全0和非全0組合成了四種特殊情況,分別表示了除了規格化數之外的四種實體,這也使得IEEE在處理浮點數操作的時候變更為靈活 非數是Kahan的一個創新,其目的是當浮點運算發生一些特殊情況的時候,軟件可以根據NaN的內容進行相應的處理,從而減少了特殊情況下軟件處理的工作量
非數分為“發信號的非數”Signaling NaN 和“靜默的非數”Quiet NaN兩類 “發信號的非數”用於在出現無效運算時發出異常信號 “靜默的非數”只記錄發生的特殊請況,而不發出異常信號,比如(+∞)±(?∞) 0?∞ 0/0 負數????√ 非數的有效部分是尾數,用於區分“發信號”還是“靜默”,並可以指明是那種異常情況產生了這個非數,從而可以根據非數的內容進行處理。對於不同異常情況對應的編碼標准沒有規定,不同的實現方案可以有不同的尾數編碼方案。 非規格化數也是一種特殊的處理方案,目的是為了避免出現下溢,從而允許用非規格化的形式來表示很小的數,而此時隱藏位就不在是 1 而是 0 了,因為已經不是規格化的范圍。這種方案也叫“逐漸下溢(Gradual Underflow)”