計算機組成.計算機在計算啥.運算與ALU

突然發現在iPad的網頁上也可以寫博客哎，，這樣就不用背著厚重的筆記本了 寫了兩句就發現，在輸入狀態下文本編輯窗口只能保持在最高，，，這樣就被虛擬鍵盤擋住了，，，體驗-1

再寫兩句發現又好了，，，體驗+1

我所認為的計算機的運算，無非就是“算數”，除了傳統的加減乘除外，在二進制的表示下，還有邏輯運算與移位運算。

而計算機真正的魅力在於，可以算得很快，所以承受得住我們去對每一個運算所賦予的詳細含義，在各種含義下的運算互相碰撞著，也就干成了各種各樣的事情。 二進制的邏輯運算對應與數學上的二元布爾代數，也是最簡單的布爾代數，說白了就是真與假，就是1和0，，，而最簡單的布爾代數已經讓電計算機如此高效，， 移位運算實際上是一種受限的乘除，即只能擴大縮小一定的倍數。比如1000右移一位成0100也就縮小了2倍，再移一位成0010又縮小了2倍，相對於最初縮小了4倍。那我想縮小三倍怎麼辦？這就是乘法和除法要做的事，其很大程度上依賴了移位運算。

---

定點數的運算

二進制的特點是，只有1和0，也就可以把“1”對應為“邏輯真”，“0”對應為“邏輯假”。 真真假假與或非，假假真真門電路 簡單的認識一下的話，計算機內把每一位也就是每個bit用一個電位體現，當這個電位有電表示1，沒電表示0。 所以說計算機為什麼非要采用二進制而不用十進制或其他進制呢？這是因為數據中的每一位需要用一位表示的話，一個電位要表示0到9的十種狀態，就要有十個電壓等級，這無疑是很復雜的。而且一位表示的信息越多，其處理起來也越復雜，而二進制只有1和0，處理起來極為簡單，當二進制保存的位也多，其處理的復雜在於多個位之間的聯系。

---

門電路

門電路干啥的？還記得1和0是用“有電”和“沒電”來表示的嗎，而門電路就是來根據有電和沒電的狀態來對1和0進行運算 什麼是運算？我說1+1=2，實際上是輸入了兩個值，分別是1和1，告訴說對著兩個數的運算是“+”，那麼我就可以得到一個輸出的結果2 每種門電路本身就對應了一種運算形式，最簡單的門電路就是與“AND”、或“OR”、非“NOT” 一般一個門電路有兩根電線作為輸入，有一根電線作為輸出
與AND：只有輸入的兩根電線都有電，輸出的電線才有電 或OR：只有輸入的兩根電線都沒電，輸出的電線才沒電 非NOT：只有一個輸入電線，輸入有電則輸出沒電，輸入沒電則輸出有電 有電、沒電、電線都是我臆想的，實現的方法我猜大概是串並聯開關啥的吧，，，作為理解尚可，而具體能否這樣實現我不知道了，，，有時間打算研究一下數字電路

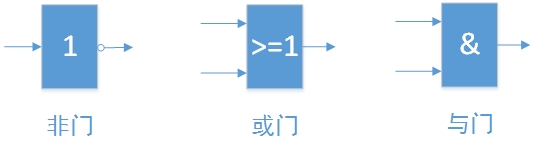
注意，非門中真正起作用的是那個小圈圈，表示取反，常與其他門電路結合表示各種更為復雜的電路

---

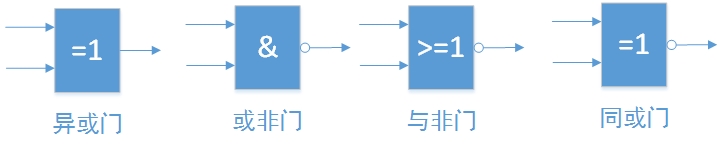
邏輯運算

邏輯非
也就是取反，1變0，0變1 由“非門”電路實現 邏輯加
就是“或”，1+1=1，1+0=1，0+1=1，0+0=0。 由“或門”電路實現 邏輯乘
就是“與”，1·1=1，1·0=0·1=0·0=0。 由“與門”電路實現 邏輯異或
“XOR”，其規則是1 XOR 1 = 0 XOR 0 = 0 ，1 XOR 0 = 0 XOR 1 = 1 解釋1:相同輸出0，不同輸出1。只適合兩個數的時候。 解釋2:參與運算的1的個數為偶數輸出0，為奇數輸出1。適合多個數進行XOR運算時候，比如1 XOR 0 XOR 1 = 0。 異或運算有很多很好的特性，沒法講，活久見

---

移位運算

移位運算就是按位平移，有的位會移到外面，那麼就丟棄，有的位會空出來 ，那麼就補0，這個絕對的“補0”是對於原碼而言的。 還是4 bit為例，二進制數“1000”，每位起個名字，最高位w3為1，依次w2為0，w1為0，w0為0
右移一位，就是讓w0取w1的值，w1取w2的值，w2取w3的值，w3沒地方取，就補0，變成了“0100”，視覺上就是“右移了一位”。 機器總是需要一個符號位來表示有符號數，而顯然符號位在移位的時候並不參與，那麼
對於有符號數的移位操作，我們叫“算數移位” 對於無符號數的移位操作，我們叫“邏輯移位” 其實無論算數移位還是邏輯移位，都是一種移位的規則，只不過只有對於各自的操作數才有意義。 顯然符號位的移位並沒有什麼意義,,,,,,當然如果有什麼特殊的手法可以讓符號位的移動產生重要的意義，那麼當然是可以移動的。 算術移位
基本規則：符號位不變，移位的空位補0 細則1：對於正數，無論機器內使用原碼、反碼還是補碼表示，其都是原碼的形式，因正數的原碼反碼補碼是同樣的表示，所以空位補0 細則2：對於負數，原碼下空位補0，反碼空位補1，補碼左移補0，右移補1 有個表格會好理解一些，依舊是4bit，最高位符號位 數值 原碼 補碼 補碼左移1位 左移後值 補碼右移1位 右移後值 2 0010 0010 0100 4 0001 1 -2 1010 1110 1100 -4 1111 -1

還有一點，就是移位的固有影響

本質上是乘、除的二進制簡化形式，左移一位即乘2，右移一位即除2 而操作的數又是整數，那麼在不斷乘2（左移）的時候很可能會超過其上限而造成結果出錯，而在不斷除2（右移）的時候很可能有會因為原數為奇數而不能正確的得出其原值*0.5的值，表現就是取整，造成精度損失 從移位的角度來看，移位的時候必然會捨棄一位，而捨棄的一位若含有原數的信息，就會造成錯誤。 至於原碼反碼補碼分別在左移右移時丟棄1還是0的時候才會出錯，，，不再細究，，，

邏輯移位：

基本規則是，無論左移右移，空位補0 無論移丟0還是1，都不影響結果的正確性和精度 沒意思，不寫了

---

加減

由於計算機引入了補碼，目的就是為了統一了正負數的運算，所以加減乘除也就要在補碼下講，當然在原碼下也同樣可講，，，

對於兩個數值X，Y（我是說數值哦）

加法：[X + Y]補 = [X]補 + [Y]補 （mod 2^n） 減法：[X - Y]補 = [X]補 + [-Y]補 （mod 2^n） 之所以要mod2^n，是因為原本長度為n位，運算之後可能會有進位導致長度變長，而實際上計算機是沒有辦法保存多出來的那一位（盡管可以采取某種特殊的手段來保存）所以就捨棄掉了。 對於減法的 [-Y]補 ，其求法為 [Y]補 的每位（包括符號位）取反後+1，即[-Y]補 = [Y]補 +1。當Y為正數時，-Y為負數，負數的補碼也就是對應正數的取反後+1，符合我們所知的轉換規則。而這條規則同樣適用於Y為負數的時候。 慣例列表 X值 [X]補 加法 Y值 [Y]補 結果值 [結果]補 2 0010 + 1 0001 3 0011 -1 1111 + 2 0010 1 0001 X值 [X]補 減法 Y值 [-Y]補 結果值 [結果]補 3 0011 - 1 1111 2 0010 2 0010 - -1 0001 3 0011

---

乘除

早期的計算機一般只有加法器和移位電路，乘法的實現依賴於加法和移位。 我們知道移位就是一種受限的乘法，左移一位相當於乘2，左移兩位相當於乘4。那麼乘法就是解決中間乘3的問題。很簡單可以想到，乘3就等於原數乘2+原數本身，也就是一次移位和一次加法來實現。 那麼這種思路可不可以形成一種公式來指導任意的乘法運算呢？ 當然是有的

---

原碼一位乘法
先在原碼下考慮，補碼的話其實會有些不同。注意原碼表示的乘數下，結果也應該是用原碼表示 先以我自己琢磨的定點整數為例，約定一下按每一位來表示的整數我寫在[ ]裡面，並用空格間隔開每位。 則A=[a3 a2 a1 a0] B=[b3 b2 b1 b0] A*B的每一位用c來表示，則c3 = a3 XOR b3，即符號位可以由兩個乘數的符號位直接得出（異或運算）從而符號位可以不用參與實際的運算過程 [c2 c1 c0] = [a2 a1 a0] * [b2 b1 b0] = [a2 a1 a0] * ( [b2 0 0] + [0 b1 0] + [0 0 b0] ) = [a2 a1 a0] * [0 0 b0] + [a2 a1 a0] * [0 b1 0] + [a2 a1 a0] * [b2 0 0] = [a2 a1 a0] * b0 * 2^0+ [a2 a1 a0] * b1 * 2^1 + [a2 a1 a0] * b2 * 2^2 注意到：
b2 b1 b0實際上就是B的每一位，而且只能是1或0，如果是0則對應項就不必運算 b0所在項需要乘2^0，也就是不需要左移 b1所在項需要乘2^1，也就是左移一位，也就是在前一項的基礎上左移一位 b2所在項需要乘2^2，也就是左移二位，也就是在前一項的基礎上左移一位 至此其實已經相當明了了，就是根據乘數B的每一位，對乘數A進行左移並加上之前的值，我們把之前的值作為部分積的概念引入
取部分積 Z0 = 0，A的絕對值記為|A| Z1 = |A| * b0 * 2^0 Z2 = |A| * b1 * 2^1 + Z1 Z3 = |A| * b2 * 2^2 + Z2 但是這樣還有個不足之處，那就是我每次進行的移位位數是遞增的，而這很容易改進，從公式就可以簡單的入手 原式 = [a2 a1 a0] * b0 * 2^0+ [a2 a1 a0] * b1 * 2^1 + [a2 a1 a0] * b2 * 2^2 = [a2 a1 a0] * b0 + 2 * ( [a2 a1 a0] * b1 + 2 * [a2 a1 a0] * b2 )
取部分積 Z0 = |A| * b2 Z1 = Z0 * 2 + |A| * b1 Z2 = Z1 * 2 + |A| * b0 語言描述下就是：
1、部分積取 |A| * b2 2、部分積左移一位 3、部分積 += |A| * b1 4、部分積左移一位 5、部分積 += |A| * b0 得到結果 再以書上所講的定點小數為例 設A=[a3 . a2 a1 a0]，B=[b3 . b2 b1 b0]，
a3和b3表示符號位 真正的純小數部分為 0. a2 a1 a0 的形式 乘積的符號依舊由 a3 XOR b3 算得 A * B = [0. a2 a1 a0] * [0. b2 b1 b0] = [0. a2 a1 a0] * ( [0. b2 0 0] + [0. 0 b1 0] + [0. 0 0 b0] ) = [0. a2 a1 a0] * b2 * 2^-1 + [0. a2 a1 a0] * b1 * 2^-2 + [0. a2 a1 a0] * b0 * 2^-3 = [0.a2 a1 a0] * b2 * 2^-1 + 2^-2 * ( [0. a2 a1 a0] * b1 + [0. a2 a1 a0] * b0 * 2^-1 ) = 2^-1 * ( [0. a2 a1 a0] * b2 + 2^-1 * ( [0. a2 a1 a0] * b1 + [0. a2 a1 a0] * b0 * 2^-1 ) ) = 2^-1 * ( |A| * b2 + 2^-1 * ( |A| * b1 + 2^-1 * |A| * b0 ) )
取部分積Z0 = |A| * b0 Z1 = 2^-1 * Z0 = Z0 右移一位 Z2 = Z1 + |A| * b1 Z3 = 2^-1 * Z2 = Z2 右移一位 Z4 = Z3 + |A| * b2 Z5 = 2^-1 * Z4 = Z4 右移一位 語言描述：
部分積取 |A| * b0 部分積右移一位 部分積 += |A| * b1 部分積右移一位 部分積 += |A| * b2 部分積右移一位 注意到 b0 b1 b2 的含義，它們是乘數 B 的每一位，而且值只能是1和0。反映到過程中講就是，如果 B 中有一位為1，那就要在“相應的兩次右移之間”部分積加上一次 |A|，如果該位為 0，部分積就可以連續右移。 小結：
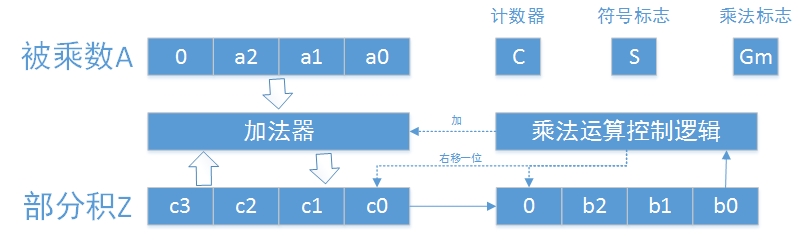
定點整數左移，定點小數右移 乘法被分解成“加上原數和移位一位”的多次重復 結合硬件的布局也許會更容易理解。一下是定點小數的硬件布局

---

補碼一位乘法
補碼一位乘法又稱為校正法，原因就是有了原碼一位乘法的基礎，補碼一位乘法只需稍作分析和校正即可轉換為原碼一位乘法來運算 以定點小數為例，並給出一張幫助理解的編碼表 編碼 一般意義下的值 視為補碼下的值 視為原碼下的值 0.00 0 0 0 0.01 0.25 0.25 0.25 0.10 0.5 0.5 0.5 0.11 0.75 0.75 0.75 1.00 1 -1 -0 1.01 1.25 -0.75 -0.25 1.10 1.5 -0.5 -0.5 1.11 1.75 -0.25 -0.75 取兩個乘數 X 和 Y均為小數 ，這裡用X和Y表示一般意義下的編碼。 所謂的一般意義就是不用符號位來保存符號，而是直接用“+”和“-”，就像我們正常寫十進制的數字的時候，正12就寫成“12”，負11就寫成“-11”。 數值 一般編碼 原碼 補碼 0.25 +0.01 0.01 0.01 -0.25 -0.01 1.01 1.11

---

模運算

在這裡我們再講一下模運算
給定一個正整數p，任意一個整數n，一定存在等式n=k?p+r 滿足k為整數，r為整數且 0 <= r < p
我們稱k為商，r為余數 所謂的模運算，也就是n mod p=r 這種形式，編程裡用 % 運算符來表示模運算，即 n % p=r 模運算規律，只介紹我們用到的兩條和我額外添加的輔助理解的簡單規則
一、(a + b)%p = (a%p + b%p) %p 二、(a * b)%p = (a%p * b%p)%p 三、a%p = (p + a)%p 四、a>0時，由上一條，(-a)%p = (p-a)%p，即一個負數模p可以等價轉換成一個正數模p，而這兩個數的絕對值之和為p

---

正文

[X]補 = x0.x1x2x3…xN-1，[Y]補 = y0.y1y2y3…yN-1 當 X 的符號任意，Y為正數的時候
[Y]補 = 0.y1y2y3…yN-1 = Y [X]補 = x0.x1x2x3…xN-1 = 2+X = 2^N +X (mod 2) 解釋一下
這裡等號“=”的意義是“編碼後長得相同” 當Y為正數的時候，Y的一般意義下的編碼形式和Y的補碼形式相同，顯然易見。 X為任意數，即可正可負。但是X是定點小數，不考慮符號的話一般意義下表示的數字范圍是[0,2)，所以對於一個數值X，其加上2後的編碼一樣，因為“2”本身已經超過了編碼的能力，即使加上了也無法被編碼，具體的表現形式就是截斷。外在表現之一就是模運算的運算規律三。
如X的值為0.25，編碼為000.01000，按表格中存儲的位來截斷之後的編碼就是0.01 X+2的值為2.25，編碼為010.01000，截斷後仍是0.01。 進一步分析，如果X為負數怎麼辦。依舊是舉例說明。
X的值為 -0.25 ， 根據表格 X的補碼形式是 “1.11” X+2的值為1.75，一般編碼的形式是“1.11” 也就是說，冥冥之中，有一種特殊的方法規律可以把我們一般意義下的編碼和補碼統一起來，簡單的+2並取模就可以轉換。 這個規律就是：對於任意小數 N，有 [N]補 = 2 + N (mod 2)，而這個規律恰又對應上了模運算的規律三，而且其實有種內在的數學聯系。 進一步的進行數學分析
[X]補 * [Y]補 = [X]補 * Y = (2^N + X) * Y (mod 2) = ( 2^N * Y (mod 2) + X * Y ( mod 2) ) (mod 2) = ( 2 (mod 2) + X * Y (mod 2) ) (mod 2) = ( 2 + X * Y) ( mod 2) = [X * Y]補 注意到中間加粗部分的轉換，即”2^N * Y (mod 2) = 2 (mod 2)”
2^N * Y 也就是對Y進行左移，還記得 Y 是 0.y1y2y3…yN-1嗎，如果左移N-1位的話，也就變成了 y1 y2 y3 … yN-1.000…0，這本身是一個大於等於1的數（注意到Y是一個正數），所以“原式 = 2 * 一個大等於1的整數 (mod 2) ”也就等於“2 (mod 2)”。其實二者在mod 2的意義下就都是0了嘛。 之所以轉換成2，而不是其他同樣是全0的編碼，是為了對應上文的規律，從而得出 [X * Y]補 這個最終結果 所以最終的結論就是：[X * Y]補 = [X]補 * Y 疑問？從推導過程中可以發現，在最後兩步的等式中，即(2+X?Y) (mod 2)=[X?Y]補 對前者運用模運算的規律的話就可以直接去掉2，從而變成了 (X?Y) (mod 2) = [X?Y]補 了啊，這很奇怪啊。。。
其實這樣的推導很對，確實可以得出這個結果，而且這個結果也確實是對的。 這裡X和Y的意義是“一般編碼”下的形式，分類討論一下的話
X為正，Y本為正，則式子顯然成立 X為負，Y為正，則 X * Y 其實是一個負值，但這還不是最終的結果，最終[X * Y]補所對應的是 (X * Y)(mod 2)，也就是身為負值的 X * Y模2之後的結果。要知道模運算的結果r總是一個大於等於0的數，所以最終[X * Y]補的編碼形式其實也就是和 (2+X*Y)的編碼形式相同。 但我們最終需要的是直接使用[X]補和[Y]補來運算得到[X*Y]補。所以我們留下了“2”，不僅僅是因為這樣做是正確的（見上條的分類討論），同時也是因為我們這樣可以轉換成我們需要的形式。 再說一遍我們的推導結論：[X * Y]補 = [X]補 * Y
這個結論意味著什麼呢？意味著我們最終需要得到的X*Y的補碼形式可以直接由X的補碼和Y的補碼（因為此時Y為正所以[Y]補=Y)形式直接參與運算得到。 具體的運算步驟和原碼的拆分一模一樣，簡單講一下
[X * Y]補 = [X]補 * 0. y1 y2 y3 … yN-1 取部分積Z0 = 0，我們最終要得到的結果是[Zn-1]補 [Z0]補 = 0 [Z1]補 = 2^-1 * （yN-1 * [X]補 + [Z0]補） [Z2]補 = 2^-1 * （yN-2 * [X]補 + [Z1]補） …… [Zn-1]補 = 2^-1 * （y1 * [X]補 + [Zn-2]補） = [X * Y]補 當X的符號任意，Y為負數的時候
我不打算推導了，，，真累 結論：[X * Y]補 = [X]補 * 0.y1 y2 y3 … yN-1 +[-X]補 最後需要加上的 [-X]補 也就是補碼一位乘法的校正值，可見校正只需要在Y為負的情況下才需要 所以實際在運算的時候，只有一個乘數是以真正的補碼的形式參與了運算，而Y則需要在判斷了符號之後去掉符號位變成正數來參與運算，Y的符號位做額外判斷是為了判斷最後是否需要加上[-X]補來進行校正 那有沒有兩個乘數都以補碼的形式直接參與運算，最後得出正確的補碼形式呢？額符靠絲

---

布斯算法“Booth算法” [X]補 = x0.x1x2x3…xN-1 [Y]補 = y0.y1y2y3…yN-1 按照校正法的結論[X?Y]補 =[X]補 ? 0.y1y2y3...yN?1 +y0 ? [?X]補 由於在mod 2的意義下，[-X]補 = -[X]補 (mod 2)
證明：證明太晦澀，我可以舉例來解釋一下
取X=0.25，則-X = -0.25。後面幾行都是二進制的形式 查表：[X]補 = 0.01 ； [-X]補 = 1.11 -[X]補 = -0.01 -0.01 (mod 2) = (10.00 - 0.01) (mod 2) = 1.11 (mod 2) = 1.11 所以有[-X]補 = -[X]補 (mod 2) 簡單說來就是，mod 2意義下，負值總要通過加2來轉化為正值，之後再談編碼形式 所以最終就有如下的形式
[X * Y]補 = [X]補 * （0.y1y2y3…yN-1）- y0 * [X]補 = [X]補 * （-y0 + y1 * 2^-1 + y2 * 2^-2 + … + yN-1 * 2^-(N-1) ) = [X]補 * [ (y1 - y0) + (y2 - y1) * 2^-1 + … + (yN-1 - yN-2) * 2^-(N-2) + (0 - yN-1) * 2^-(N-1) ] = [X]補 * [ (y1 - y0) + (y2 - y1) * 2^-1 + … + (yN-1 - yN-2) * 2^-(N-2) + (yN - yN-1) * 2^-(N-1) ] 式中”yN = 0” 如此再結合部分積
取部分積Z0 = 0 Z1 = 2^-1 * {Z0 + (yN - yN-1) * [X]補 } Z2 = 2^-1 * {Z1 + (yN-1 - yN-2) * [X]補 } …… ZN-1 = 2^-1 * { ZN-2 + (y2 - y1) * [X]補 } ZN = ZN-1 + (y1 - y0) * [X]補 = [X * Y]補 [X]補直接參與了運算，y0也參與了運算也就意味著Y也是以補碼的形式[Y]補直接參與了運算 特點
首先是X和Y均是以補碼的形態[X]補和[Y]補參與了運算 結果是[X*Y]補 運算期間的邏輯變得復雜了，原先只需要看Y的對應位是1和0，而現在每一步需要用到Y的兩位之間的差，見下面的表格 最後一步是不需要乘2^-1，也就是不需要右移 yi-1 yi yi - yi-1 操作 0 0 0 加上0，然後右移一位 0 1 1 加上[X]補，然後右移一位 1 0 -1 加上[-X]補，然後右移一位 1 1 0 加上0，然後右移一位

---

除法運算
因為考試不考，，，所以先不細寫了，，簡要講一下我對除法的理解 想象一下十進制下手算除法的過程，總是要去湊出每一位，使其與除數相乘的結果剛好不大於下面的被除數。每次湊數的時候都需要乘乘看到底是不是剛好不大於被除數。 那麼在二進制下也是湊的嗎？不，這可是神奇的二進制 因為二進制只有0和1，所以假如在二進制下模仿十進制除法的姿態，我們去湊數的時候也只有0和1兩種選擇
如果0是正確的結果，這也就意味著除數大於被除數 如果1是正確的結果，這也就意味著除數小於被除數 也就是說，在二進制下，我們不需要湊數，只需要比較一下除數和被除數那個大，就可以知道當前數位上是填0還是填1了。 比較好比啊，只需要兩個數減一減就知道誰大誰小了。 再配合上移位操作，除法也就被完美的用減法和移位實現了。 嗯。神奇的二進制。 具體的方法有
原碼恢復余數除法
核心思想就是：每次在做減法看誰大誰小來決定填1還是0的時候，我們並不知道到底誰大誰小。 看誰大誰小，就需要看減完的余數是正還是負 如果余數為負，就說明我們減過頭了，自然是填0，但是我們還需要再把余數恢復過來，也就是所謂的“恢復余數” 原碼加減交替除法 核心思想就是：改進了原碼恢復余數除法，不需要恢復余數。 本質上我們不需要死板的看余數的正負才能判斷誰大誰小，
在余數為負的時候，我們可以通過加上除數而不是恢復余數後再去除數，一樣可以判斷誰打誰小來進一步判斷填1還是0 余數為正的時候自然就是減去除數 所謂加減交替

---

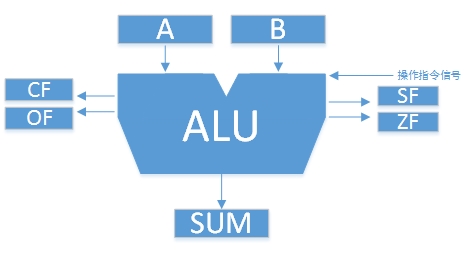
ALU

算術邏輯單元（arithmetic and logic unit） 組成：
內部組成：
加法器AU 邏輯運算器 移位器 求補器 外部組成：
兩個輸入緩沖器A和B 輸出緩沖器SUM 進位標志CF、溢出標志OF、符號標志SF、零標志ZF

---

加法器

加法器比較好講，也比較簡單 所以大概這就是被選入教材的原因

---

串行加法器

考慮我們手算加法的時候，總是
先個位相加，選出結果和進位 再十位相加並加上進位，再算出結果和進位 …… 這個就是一個鏈式的過程，每一位（除了第一位）之外其結果的得出都依賴於前一位的進位，並且該位運算完的進位需要提供給下一位才能得出下一位的結果和進位，下一位的進位再…… 基本邏輯單元：全加器FA（Full Adder）

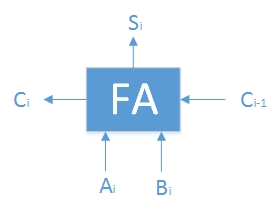
介紹
兩個本位加數 Ai 和 Bi 低位進位 Ci-1 本位和 Si 向高位的進位 Ci Si = Ai XOR Bi XOR Ci-1 Ci = Ai·Bi + (Ai+Bi)·Ci-1（邏輯加OR 與 邏輯乘AND） 記Gi=Ai·Bi稱為本位進位 記Pi=Ai+Bi稱為傳遞條件，Pi·Ci-1稱為傳遞進位 可見：Ci = Gi + Pi·Ci-1 多個FA串接起來，就組成了串行加法濃ky"http://www.2cto.com/kf/ware/vc/" target="_blank" class="keylink">vcgzNi14zxiciAvPg0Kxve8/rWl0rujqL32RkGjqbPJsb61zSDL2bbIwv2jrKOso6zP68/rvs3SqsL9y8DByw0KPGhyIC8+DQo8aDUgaWQ9"並行加法器">並行加法器 我們看到，每一位之間的依賴關系，是“進位值Ci” 如果我們能提前知道了每一位的 Ci，那麼位之間的依賴關系也就不復存在了，也就可以並行進行了，就是同時算所有的數位

有辦法嗎？有的

以四位CRA（Carry Ripple Adder）為例

C0 = 0 C1 = G1 + P1·C0 C2 = G2 + P2·C1 C3 = G3 + P3·C2 C4 = G4 + P4·C3 進一步變換可得到
C0 = 0 C1 = G1 + P1·C0 C2 = G2 + P2·G1 + P2·P1·C0 C3 = G3 + P3·G2 + P3·P2·G1 + P3·P2·P1·C0 C4 = G4 + P4·G3 + P4·P3·G2 + P4·P3·P2·G1 + P4·P3·P2·P1·C0 容易看出，雖然邏輯復雜了很多，但是Ci只和G、P、C0有關，而不依賴於Ci-1，而G、P有只和各自的Ai、Bi有關 這也就意味著，我們一開始就知道的Ai、Bi和C0=0，足以求出C1、C2、C3、C4。這樣不就是“提前把所有的Ci”求出來了嘛 我們就設計了這樣的邏輯電路，輸入是G1、P1、G2、P2、G3、P3、G4、P4、C0，依照公式設計好電路，輸出是C1、C2、C3、C4，分別輸入到對應的全加器FA中。 這就是先行進位加法（Carry Look Ahead， CLA）鏈，也叫超前進位鏈

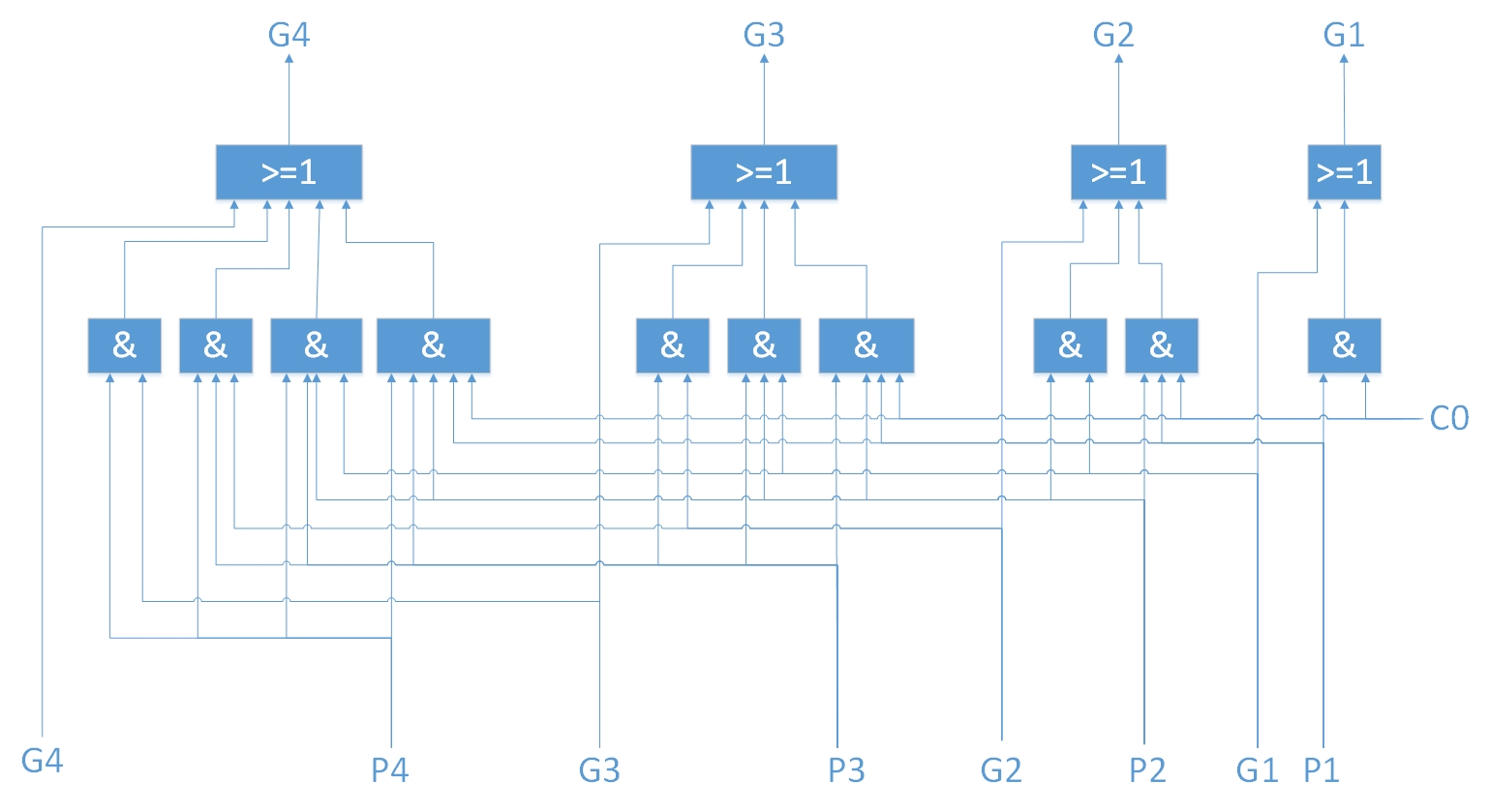
四個FA和一個CLA就可以組成一個四位的先行進位加法器，SN74181就是這樣一種ALU芯片

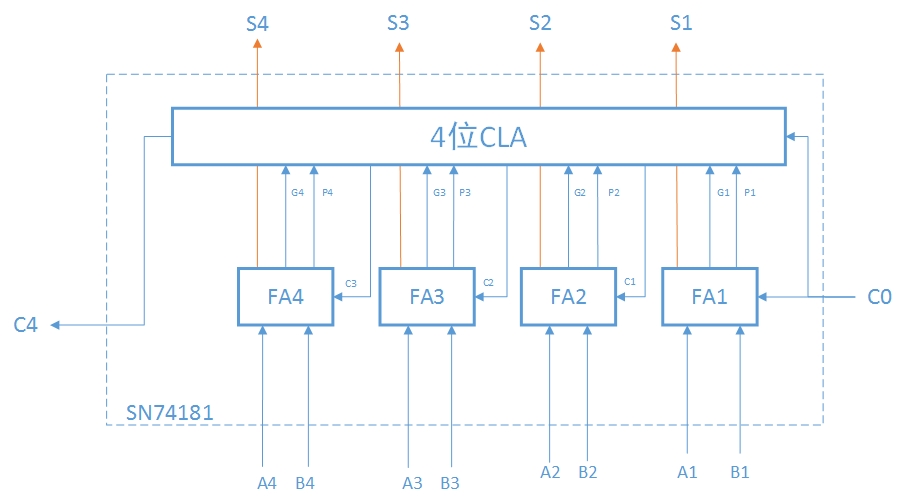
至此也就了解了基本的並行思想 然而多個SN74181之間仍然需要串行，，嗯哼，我猜你想到了什麼。沒錯，可以用同樣方法來對多個SN74181進行並行化
D1 = G4 + P4·G3 + P4·P3·G2 + P4·P3·P2·G1 T1 = P4·P3·P2·P1 則 C4 = D1 + T1·C0 C8 = D2 + T2·D1 + T2·T1·C0 C12 = D3 + T3·D2 + T3·T2·D1 + T3·T2·T1·C0 C16 = D4 + T4·D3 + T4·T3·D2 + T4·T3·T2·D1 + T4·T3·T2·T1·C0 和之前很是對稱的形式，只不過D和T是由G和P來生成 ，而G和P是直接由A和B來生成。實際上實現的邏輯電路完全一樣，但是
前者CLA提前生成的是FA之間的進位信號，我們稱之為組內信號 而此時提前生成的是SN74181之間的進位信號 ，稱為組間信號 我們稱此時實現的邏輯電路為成組先行進位（Block Carry Look Ahead，BCLA）鏈 SN74182就是一個BCLA部件。
注意和SN74181的含義並不對稱 等等我就不畫圖了，基本思路知道就好，按理可以無限的並行下去，但問題是1）我們不一定需要那麼多位的運算，2）雖然是模塊化 設計但避免不了復雜度的提高，不過這種越往上並行所需要的部件就越少，就部件數量來說並不會增加很多。

---

浮點數運算

這個就很簡單

加減

按部就班的來，不過我想你也應該有思路
1、對階：使兩個操作數 階碼相同 2、尾數求和：對尾數進行加減運算 3、規格化：規格化運算的結果 4、捨入：為保證精度，考慮尾數右移的時候丟失的數值是否需要捨入（相當於十進制下的四捨五入） 5、溢出判斷：上溢下溢還是沒溢出 列舉一下捨入的策略
截斷法：直接捨棄丟失的數值 0捨1入法：丟失0就直接丟棄，丟失1就置最低位為1（對原碼所言）。補碼下自然應是“1捨0入”了） 恆置1法：也叫“馮·諾依曼捨入法”，無論丟失0或1，永遠置最低位為1。簡單但是誤差大 查表捨入法：用ROM存一張表，以尾數的最低K位和丟失的最高位作為地址，查找出的數值來代替尾數的最低K位。提前設計好。由於讀取ROM要比直接進行加法快，所以速度快。但又增加了硬件。

乘除

自己想象怎麼算。嗯，很簡單吧。 1、階碼相加、減 2、尾數相乘、除 3、規格化 4、捨入處理 5、溢出判斷